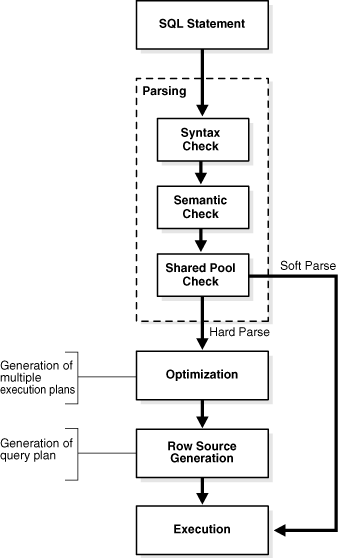
Query Evaluation
The processing of an SQL query is delegated to 3 programs:
- Parser: translates the SQL query into an internal query representation based on relational algebra
- Query Optimizer: determines the most efficient way to execute the query, i.e. determines an efficient execution plan
- Plan Executor: executes the plan and returns the result to the user
Queries are composed of a few basic operators:
- Selection: filters the tuples based on a condition
- Projection: selects specific attributes from the tuples
- Order By: orders the tuples based on a specific attribute
- Join: combines the tuples of two queries based on a common attribute
- Group By: groups the tuples based on a specific attribute and applies an aggregate function to each group
- Intersection: returns the tuples that are present in both queries
- etc...
Cost model and notation
There are multiple ways of implementing each relational operator, thus we must estimate how expensive a specific execution is to be able to choose the most efficient. As a general back of napkin calcuation, we will compare performance based on number of I/O i.e pages retrieved from disk. We make a few simplifying assumptions:
- the root and intermediate nodes of the B+ tree are in main memory
- leaf nodes and data pages are not in memory
Schema for our example
Users (uid: int, uname: string, experience: int, age: int)
GroupMembers (uid: int, gid: int, stars: int)
Users(U):
| GroupMembers(GM):
|
Selection
SELECT *
FROM Users
WHERE uid = 123
Reduction factor
The reduction factor of a condition is the ratio of the number of tuples in the result to the number of tuples in the original table. It is used to determine the efficiency of the query; the higher the reduction factor, the more efficient the query is. Given a relation , it can be expressed as
ExampleAssume there are 10 different experience levels for User, and we want to calculate the reduction factor for the condition when the user has experience of 5. it can be calculated as:
When calculating execution efficiency, the value of is not known, so a common solution is for the DBMS to keep track of the number of different values and assume a uniform distribution. This is done through various methods e.g indices, heuristics, histograms, etc.
Execution Options:
- Simple scan on data pages
- always possible, even with indices
- I/O cost = # of data pages
- if search on primary key, average I/O cost = 1/2 # of data pages
- Use an index on the condition attribute
- Case 1. clustered index tree
- Case 2. non-clustered index tree
Clustered Index tree
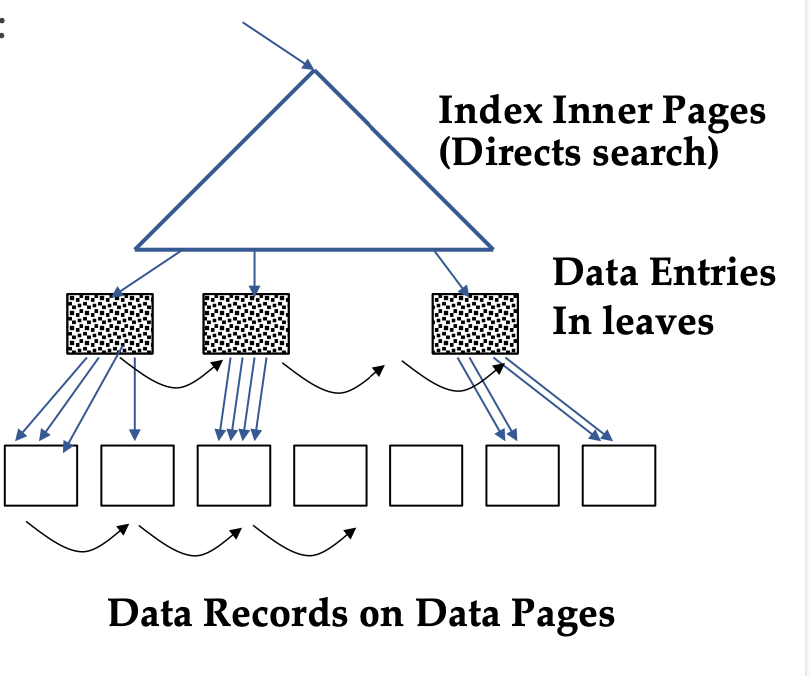
Step 1. Go from the root to the left-most leaf lq with qualifying data entry.
- cost = one I/O to retrieve lq page
Step 2. retrieve page of first qualifuing tuple within lq leaf.
- cost = one I/O
Step 3. keep moving to adjacent leaves as long as search criteria is fulfilled. Each move to an adjacent leaf is an additional I/O
- Since clustered, each data page is only retrieved once.
- cost = proportion of tuples that match is roughly equal to proprtion of data pages that match - if ~20% of tuples qualify then ~ 20% of data pages are retrieved.
SELECT * FROM Users WHERE uid = 123
Since uid is the primary key, only one tuple will match, thus I/O cost = cost of step 1. = retrieve lq page + retrieve corresponding data page = 2
ExampleSELECT * FROM Users WHERE uname = "John"
Let's assume there are 100 matching tuples for the query. Since we know for users there are around 80 tuples/page, the matching tuples will be spread across 2 pages. Therefore the I/O cost will be lq + 2 data pages = 3
ExampleSELECT * FROM Users WHERE uname < 'G'
Let's assume there are 10000 matching tuples for the query. That means 25% of the tuples are a match, which means we will need to access roughly 25% of the memory pages. Therefore the I/O cost will be lq + 125 data pages = 126
Note: some systems might retrieve all rids through the index (not efficient). – In this case, example 3 will read approx. 25% of the leaf pages.
Non-clustered Index tree: standard strategy
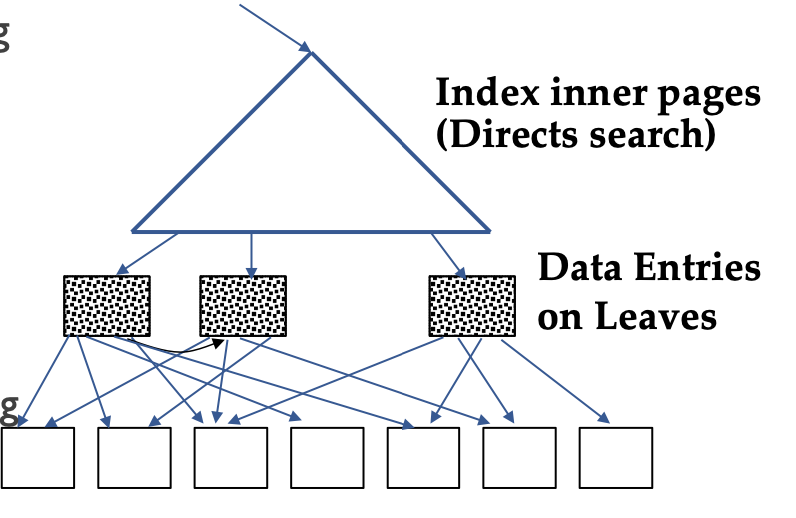
Step 1. Go from the root to the left-most leaf lq with qualifying data entry.
- cost = one I/O to retrieve lq page
Step 2. retrieve page of first qualifuing tuple within lq leaf.
- cost = one I/O
Step 3. keep moving to adjacent leaves as long as search criteria is fulfilled. Each move to an adjacent leaf is an additional I/O
- Since non-clustered, each new tuple might be in a different memory page.
- cost = no correlation between page I/O cost and number of tuples retrieved. worst case scenario is need to do a new page I/O per tuple.
Non-clustered Index usually only useful with very small reduction factors
Non-clustered index: Sorting strategy
- Determine all leaf pages that have matching entries
- sort the matching data entries by their page-id
- Retrieve each memory page only once and get all matching tuples
The advantage is that the worst case scenario is upper bounded by # of data pages + # of leaf pages. We will never need to make an I/O multiple times for one memory page since the entries are sorted by their page-id. Thus depending on how the tuples are distributed among the memory pages, it is possible to be more efficient than a simple scan.
Selection on 2 or more attributes
Let's say we are making a selection query for all tuples whose attribute A =100 and attribute B = 50, and our relation has 500 pages.
Option 1. No index
- simple scan: 500 pages, 1 I/O for each page -> 500 I/Os
Option 2. Index on A
- get all the tuples where A=100 through the index, and then check their B value
- cost = cost to query for A=100
Option 3. Create 2 indexes; one for each attribute
-
- get all the tuples where A=100 through the A index,
-
- get all the tuples where B=50 through the B index
-
- build and return an intersection of all the tuples
- cost = cost to query for A=100 + cost to query for B=50
Now lets consider a selection query for A=100 OR B=50
Option 1. No index
- simple scan: 500 pages, 1 I/O for each page -> 500 I/Os
Option 2. Index on A
- Not useful, since it is an OR condition
Option 3. Create 2 indexes; one for each attribute
- get all the tuples where A=100 through the A index
- get all the tuples where B=50 through the B index
- Build and return the union of the tuples
- cost = cost to query for A=100 + cost to query for B=50
Main memory usage note
- A scan over a relation only needs two main memory frames: 1 for output, 1 for input
- Index tree additionally needs to hold root and intermediate pages, and space to retrieve one leaf page at a time
- Index tree with sorting/intersection additionally needs to hold root and intermediate pages, as well as necessary leaf pages for sorting/intersection.
Projection
SELECT uid, experience
FROM Users
projection is often used together with other operators in one query
SELECT uid, experience
FROM Users
WHERE experience > 5
For projection, decide how to do the other operations first, and then do the projection on the fly.
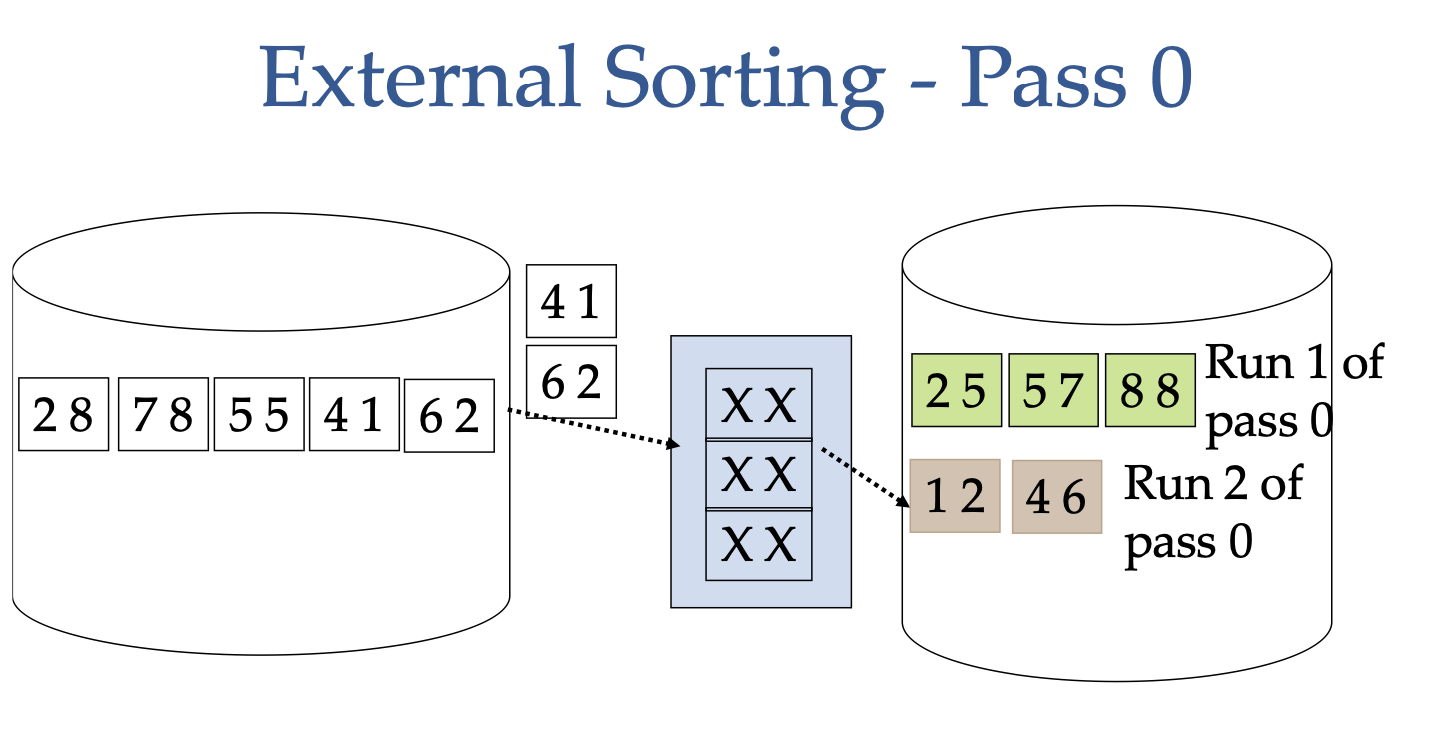
External Sorting
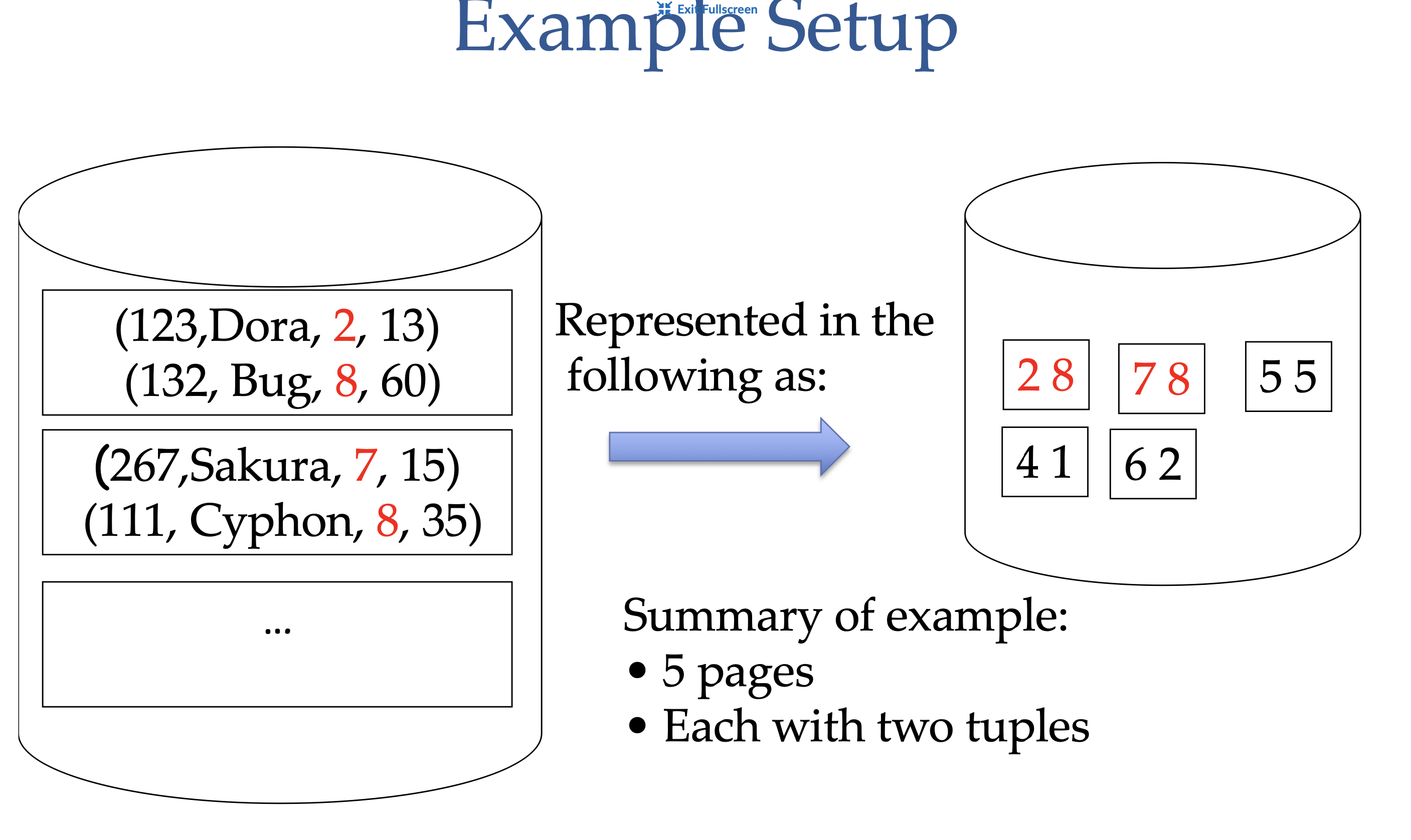
Say we would like to sort 5 pages of data, each with two tuples, and we only have 3 buffer frames available to us. The way we can do this is:
- Load 3 pages into the buffer frames
- Sort the tuples in the buffer frames
- Write the sorted tuples to disk (this is one run)
- Repeat steps 1-3 for the remaining pages (this is one pass)
The cost = 1 I/O per page to load into the buffer frames, and 1 I/O per page to write to disk = 2(# of pages) for pass 0
Once we have each run sorted, we can merge them together to get the final sorted result. This can be done with just a linear merge, comparing the smallest elements between the runs and picking the smallest each time.
The cost = 1 I/O per page to merge the runs, and typically the output is given directly to the client so there is no additional write I/O, i.e. cost = (# of pages) for Pass 1
The general I/O cost is given by the formula
Where is the number of pages.
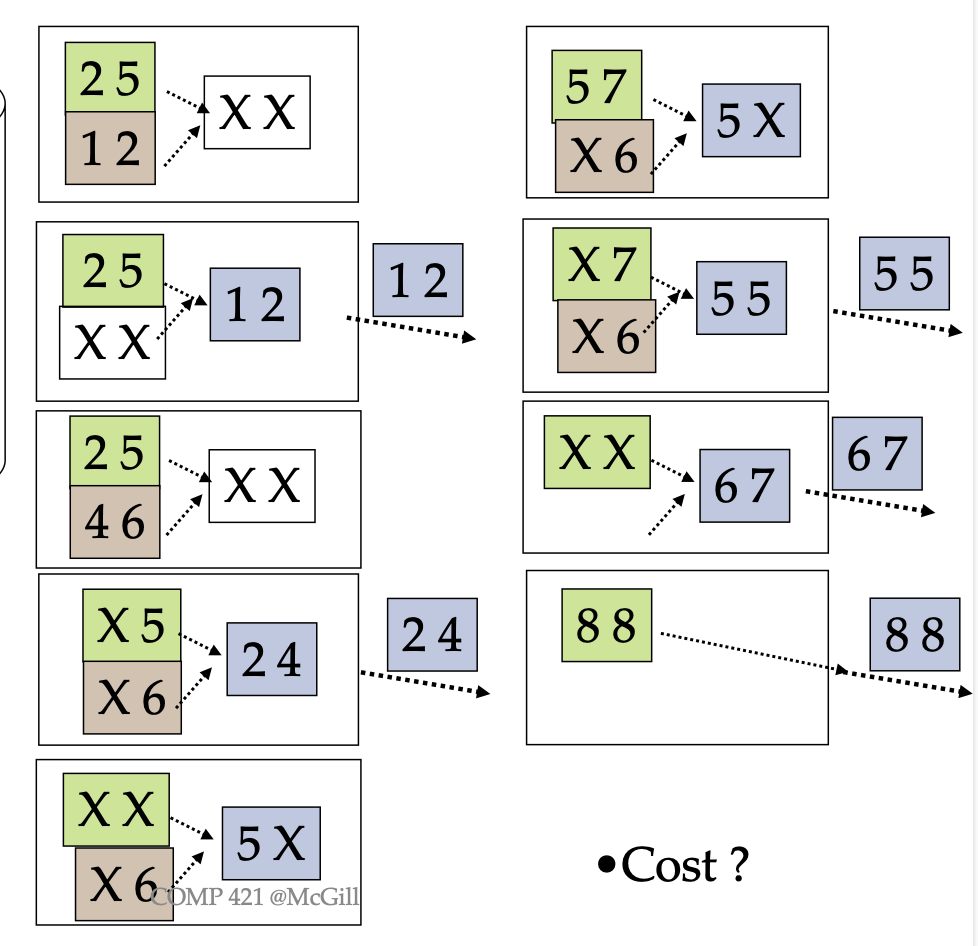
Sometimes, a second pass is needed if pass 0 creates more runs than there are main memory buffers. A general solution to calculate # of passes needed is:
where is the number of pages, and is the number of buffer frame.
Joins
SELECT *
FROM Users U, GroupMembers GM
WHERE U.uid = GM.uid
Note: Users U is the outer relation and GroupMembers GM is the inner relation
Cardinality of Users ⋈ GroupMembers = |GroupMembers|
- Join attribute is primary key for Users, and foreign key in GroupMember, so each GM tuple will match with exactly one User tuple
Cardinality of Users ✕ GroupMembers = |Users| * |GroupMembers|
- Cross product is always the product of individual relation sizes
Below detail the many ways of executing a join
Simple Nested Loop Join
For each tuple in the outer relation, we scan each tuple in the inner relation.
foreach tuple u in U do
foreach tuple gm in GM do
if u.uid = gm.uid then
add <u, gm> to result
I/O cost =
- |OuterPages| comes from the cost of scanning each tuple in Users which is the # of pages in Users.
- |OuterRelation|*|InnerPages| comes from the cost of scanning each tuple in GroupMembers which is |InnerPages| and we do this for each tuple in Users, so we multiply by |OuterRelation|
Page Nested Loop Join
For each page of Users U, get each page of GroupMembers GM and output <u,g> where u is in and g is in
foreach page pu of Users U
foreach page pg of GroupMembers GM
foreach tuple u in pu do
foreach tuple g in pg do
if u.uid = g.uid then
add <u,g> to result
I/O cost =
- |OuterPages| - cost of scanning each page in Users
- |OuterPages|*|InnerPages| - cost of scanning each page in GroupMembers is |InnerPages|, and we do this for each page in Users, so we multiply by |OuterPages|
Notice that for simple nested loop join and page nested loop join, we only need 3 memory frames; 1 for a page of U, 1 for a page of GM, and 1 for the result.
Block Nested Loop Join
For each block of pages of Users U, get each page of GroupMembers GM, and write out matching pairs <u,g> where u is in and g is in
Notes: 1 block of pages from Users U and one page of GM must be able to fit in main memory
foreach block b of Users U do
foreach page pg of GroupMembers GM do
foreach tuple u in b do
foreach tuple g in pg do
if u.uid = g.uid then
add <u,g> to result
I/O cost =
- |OuterPages| = cost of scanning each block in Users which is the # of pages in Users.
- = number of blocks, and for each block we load inner pages, so we multiply by
In this case, the memory requirement is the size of a block of pages of Users U + 1 frame for the GM page + 1 output frame.
Best case cost is if the entire outer relation fits in main memory, making the I/O cost = |OuterPages|+|InnerPages|
Index Nested Loops Join
For each tuple in the outer relation Users U, we find the matching tuples in GroupMembers GHM through an index on the join attribute.
foreach tuple u in U do
find all matching tuples g in GM through index
foreach matching g in GM do
add <u,g> to result
I/O cost =
- = cost of scanning each tuple in Users
- = cost of retrieving matching inner tuples
When compared to block nested loop, index nested loop has less I/O cost if |OuterRelation| is very small.
Sort Merge Join
Sort the outer relation and the inner relation by the join attribute. Then do a 2-pointer approach, doing a linear scan over the two relations and output matching tuples.
sort U by uid
sort GM by uid
u,g = the first tuples in U and GM
while U or GM is not empty do
if u.uid = g.uid then
output <u,g>
u,g = the next tuples in U and GM
else if u.uid < g.uid then
u = the next tuple in U
else
g = the next tuple in GM
The cost of the merge step is simply the cost of loading the two relations, which is |UserPages|+|GroupPages|
The cost of the sorting step we know using the formula from the external sort section is (2(2)-1)|UserPages| + (2(2)-1)|GroupPages| -- we can assume it can be sorted in 2 passes
Final I/O cost = cost of sorting + cost of merge =
However, we can pipeline the sorting and merging step, such that instead of needing to load the two relations into memory for the merge which would cost |UserPages|+|GroupPages|, we can somehow do the merge step in place, saving us the cost of loading the two relations into memory.
Thus the final optimized I/O cost is
Distinct Projection
SELECT DISTINCT uname
FROM USER
To eliminate duplicates, we need to sort the relations by the projection attribute. This step is usually done at the very end of the query to minimize number of tuples that need to be sorted, or if the relation is already sorted for another operator. It is an expensive operation so when writing queries, only use when absolutely necessary.
Set Operations
The same idea as the previously discused equality join operations.
Aggregate Operations
- Without Grouping: typically requires scanning the entire relation
- With Grouping: sort on the group-by attribute, and then scan the relation while computing the aggregate for each group.